Collaborators: Prof Sebastian Skatulla (University of Cape Town), Prof Ntobeko Ntusi (University of Cape Town), Prof Freedom Gumedze (University of Cape Town, Prof Richard Naidoo (University of Cape Town) and Dr Jagir Hussan (University of Auckland)
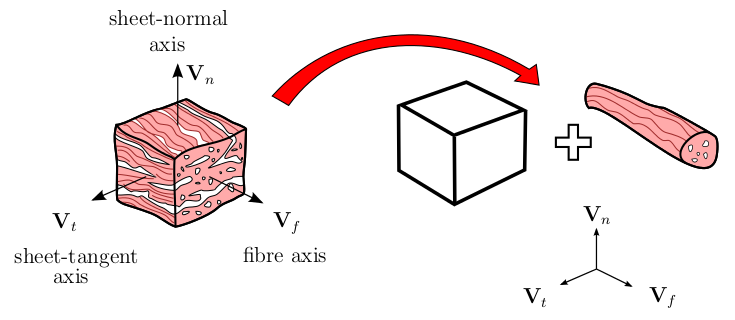
Figure 1: Modelling of the micro-structural composition of muscle tissue consisting of muscle fibres embedded in a constraining collagen fibre network.
Summary:
Myocardial tissue is a complex heterogeneous material characterized by different muscle fibre hierarchies interwoven by collagen, elastin, coronary capillaries and various proteins. For instance, fiber orientation, dispersion, thickness, length and relative volume fraction have a considerable local character. The myocardium is a laminated structure with a complex hierarchical organization. These approximately four to six cells thick layers or myocardial sheets are loosely interconnected by perimysial collagen fibers which are able to slide over one another with a relatively low slippage resistance. Moreover, the initially crimped and coiled collagen fibers straighten during passive filling. Another consideration is that for small and intermediate levels of strain the myocardial material response and its stiffness is dominated by kinematics of the myocytes or bundles of myocytes. These are linked to the collagen matrix but remain highly deformable in terms of axial and associated transversal deformation as well as torsional and flexural deformation. Only for larger strains, further myocyte deformation is prevented by the cross-linked collagen network which is significantly stiffer than the myocytes. It is therefore the former which takes over dominating the material behaviour of myocardial tissue.
In this research, the myocardial material response is obtained from the micro-structural level where it originates. Two different avenues are pursued: (i) generalised continuum methods and (ii) FE-square-based modelling. In case of (i), the fibrous characteristics of the myocardium are modelled by higher-order continua, such as the Cosserat-fibre or the micromorphic-fibre continuum. Both additionally allow for the inclusion of non-local effects due to the heterogeneous material composition at smaller scales. Specifically, the non-local material response is linked to higher-order deformation modes and extra degrees of freedom associated with twisting and bending of an assembly of muscle fibres arising from hierarchical multi-scale features within a representative volume element (RVE). In this sense, a scaling parameter characteristic for the tissue’s underlying micro-structure, becomes a material parameter of the formulation. As the anisotropic material composition of the myocardium throughout the heart is highly non-uniform, the ability to implicitly account for scale-dependent torsion and bending effects in the constitutive law gives this approach an advanced material description over classical formulations. In case of (ii) we want to utilize FE-square modelling which considers finite element discretizations of the material at two scales, the micro and the macro-scale. In this way, the actual micro-structural material composition can be taken into account and by means of solving a boundary value problem an accurate micro-structural stress distribution.
