Advancing hybrid techniques for efficient CFD calculations
Finite difference methods are known to be an efficient choice in many CFD tasks where a high order of accuracy is desired. Examples include the efficient resolution of viscous boundary layers over smooth surfaces, as well as long distance wave propagation and advection. The general concept of summation-by-parts operators has proven itself as an excellent framework for the derivation of stable numerical conditions, both at physical boundaries and between computational blocks.
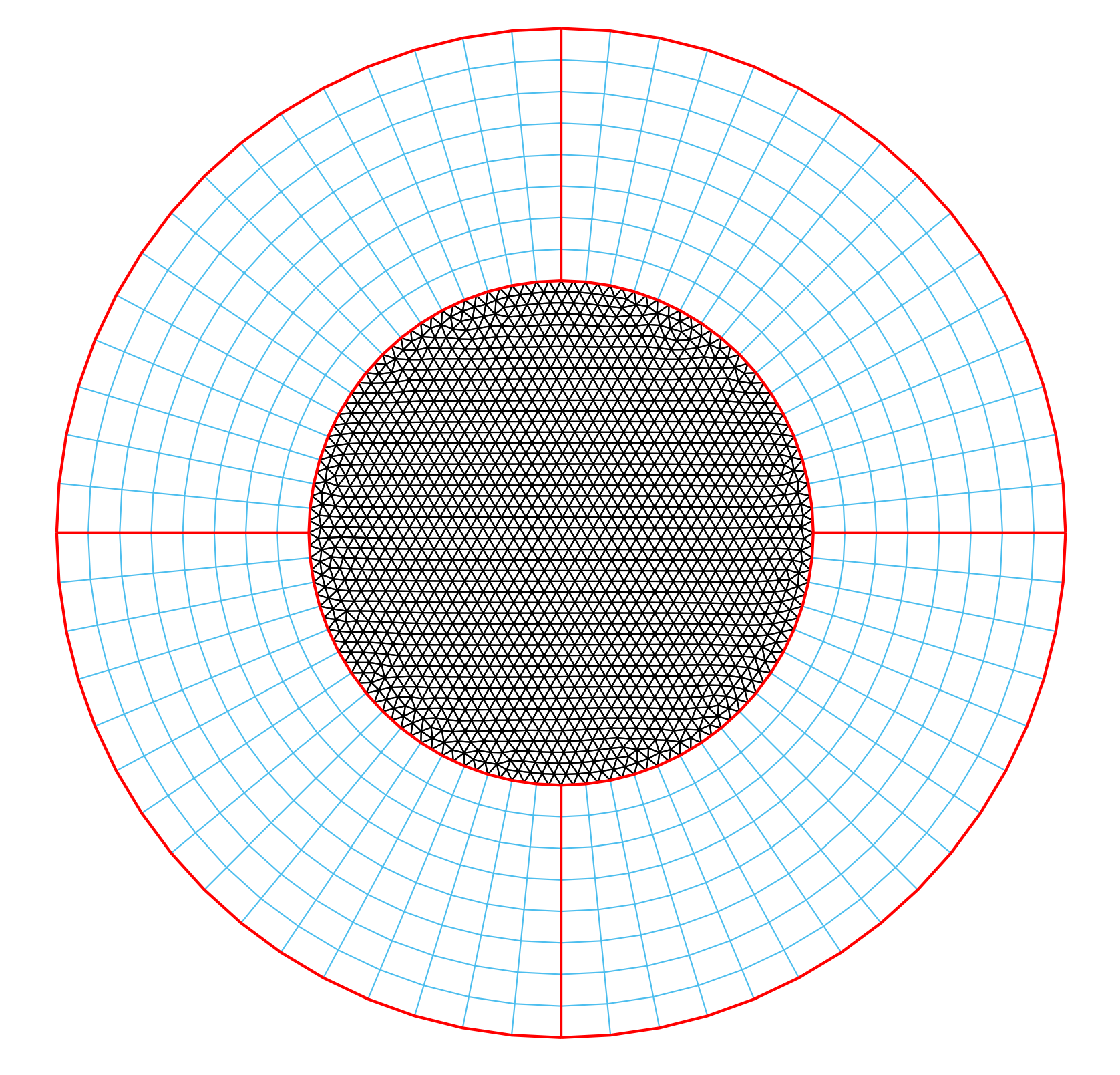
Based on the summation-by-parts concept, Tomas Lundquist is developing a hybrid methodology for the coupling of high order finite difference blocks to a general form of surrounding unstructured finite volume mesh. The goal is to combine provable linear stability with the smallest possible discretization errors. The new methodology is to be applied for combining the two codes ESSENSE (high order structured) and ELEMENTAL (unstructured ) in a way that is maximally flexible, robust and efficient. The target is to drastically reduce the computational cost in compressible flow calculations around the NASA CRM 3D airframe, including aeroelastic gust modelling, turbulence, and vortex interactions in formation flight.